接下来会有一系列文章讲解Python机器学习库:scikit-learn。本文是第一篇,我们会介绍一些基本概念以及讲解如何使用scikit-learn进行线性回归分析。
scikit-learn介绍
scikit-learn是Python语言的机器学习软件库。其官网地址在这里:scikit-learn。
scikit-learn有如下特点:
- 它包含了简单高效的数据挖掘和数据分析工具
- 可供所有人使用,并可在各种环境下使用
- 基于NumPy,SciPy和matplotlib
- 基于BSD开源,因此开源项目和商业项目均可以使用
在使用scikit-learn编程的时候,我们也经常会用到NumPy,pandas和matplotlib,因此建议读者先对这几个库有一些了解。我之前也写过几篇相关文章:
机器学习简介
通常情况下,机器学习包含了一组样本数据的集合。学习的目的在于通过对已知数据的分析来预测未知的数据。
如果每个样本包含不止一个数字,则说数据具有多个属性或特征。
学习问题可以进行如下的分类:
- 监督学习(Supervised Learning):数据包含了我们将要预测的附加属性。监督学习又可以分为:
- 分类(Classification):样本属于两个或多个类别,我们希望从已标记的数据中学习如何预测未标记数据的类别。分类问题的一个例子是手写数字识别的例子,其中的目标是将每个输入向量分配给有限数量的离散类别之一。
- 回归(Regression):如果预测的结果由一个或多个连续变量组成,则该任务称为回归。回归问题的一个例子是预测某个动物的长度与年龄和体重的关系。
- 无监督学习(Unsupervised Learning):其中训练数据由一组没有任何相应目标值的输入向量x组成。这些问题的目标可能是发现数据中类似例子的集合,这称为集群(clustering),或确定输入空间内的数据分布,这称为密度估计(density estimation),或者从高维度投影数据将空间降低到二维或三维。
实验环境
本文的代码在如下环境中测试:
- Apple OS X 10.13
- Python 3.6.3
- scikit-learn 0.19.1
- matplotlib 2.1.1
- numpy 1.13.3
本文中的源码和测试数据可以在这里获取:sklearn_tutorial
实验描述
在本文中,我们将进行房价的预测。
使用的数据是一组包含了若干房价信息的CSV文件。可以在这里获取这个文件:housing.csv。
注:sklearn_tutorial项目源码中也包含了这个数据文件。
我们可以通过下面的代码读取这个文件:
import pandas as pd
input_data = pd.read_csv("./housing.csv")
注:本文中,假定读者已经对NumPy,pandas和matplotlib三个库有基本的了解。
了解数据
在我们拿到数据之前,我们通常会先对数据对一些大致的了解。
例如这样:
print("Describe Data:")
print(input_data.describe())
print("\nFirst 10 rows:")
print(input_data.head(10))
describe()是pandas提供的API,它会输出对于数据整体的统计描述信息,像下面这样:
Describe Data:
longitude latitude housing_median_age total_rooms \
count 20640.000000 20640.000000 20640.000000 20640.000000
mean -119.569704 35.631861 28.639486 2635.763081
std 2.003532 2.135952 12.585558 2181.615252
min -124.350000 32.540000 1.000000 2.000000
25% -121.800000 33.930000 18.000000 1447.750000
50% -118.490000 34.260000 29.000000 2127.000000
75% -118.010000 37.710000 37.000000 3148.000000
max -114.310000 41.950000 52.000000 39320.000000
total_bedrooms population households median_income \
count 20433.000000 20640.000000 20640.000000 20640.000000
mean 537.870553 1425.476744 499.539680 3.870671
std 421.385070 1132.462122 382.329753 1.899822
min 1.000000 3.000000 1.000000 0.499900
25% 296.000000 787.000000 280.000000 2.563400
50% 435.000000 1166.000000 409.000000 3.534800
75% 647.000000 1725.000000 605.000000 4.743250
max 6445.000000 35682.000000 6082.000000 15.000100
median_house_value
count 20640.000000
mean 206855.816909
std 115395.615874
min 14999.000000
25% 119600.000000
50% 179700.000000
75% 264725.000000
max 500001.000000
而input_data.head(10)输出了数据的前10行。
First 10 rows:
longitude latitude housing_median_age total_rooms total_bedrooms \
0 -122.23 37.88 41.0 880.0 129.0
1 -122.22 37.86 21.0 7099.0 1106.0
2 -122.24 37.85 52.0 1467.0 190.0
3 -122.25 37.85 52.0 1274.0 235.0
4 -122.25 37.85 52.0 1627.0 280.0
5 -122.25 37.85 52.0 919.0 213.0
6 -122.25 37.84 52.0 2535.0 489.0
7 -122.25 37.84 52.0 3104.0 687.0
8 -122.26 37.84 42.0 2555.0 665.0
9 -122.25 37.84 52.0 3549.0 707.0
population households median_income median_house_value ocean_proximity
0 322.0 126.0 8.3252 452600.0 NEAR BAY
1 2401.0 1138.0 8.3014 358500.0 NEAR BAY
2 496.0 177.0 7.2574 352100.0 NEAR BAY
3 558.0 219.0 5.6431 341300.0 NEAR BAY
4 565.0 259.0 3.8462 342200.0 NEAR BAY
5 413.0 193.0 4.0368 269700.0 NEAR BAY
6 1094.0 514.0 3.6591 299200.0 NEAR BAY
7 1157.0 647.0 3.1200 241400.0 NEAR BAY
8 1206.0 595.0 2.0804 226700.0 NEAR BAY
9 1551.0 714.0 3.6912 261100.0 NEAR BAY
从上面的输出中,我们对数据有了不少的了解:
- 这组数据总计包含了20640条数据。
- 数据分为longitude,latitude,housing_median_age,total_rooms,total_bedrooms,population,households,median_income,median_house_value,ocean_proximity一共10列。
- 有些数据缺少total_bedrooms列的信息,因此其总共的有效数据只有20433条
- ocean_proximity的数据是字符串类型的,而其他列都是数字类型的
- median_house_value代表了房子的价值,这就是我们希望预测的数据
我们也可以借助于matplotlib进行可视化结果的展示。
例如这样:
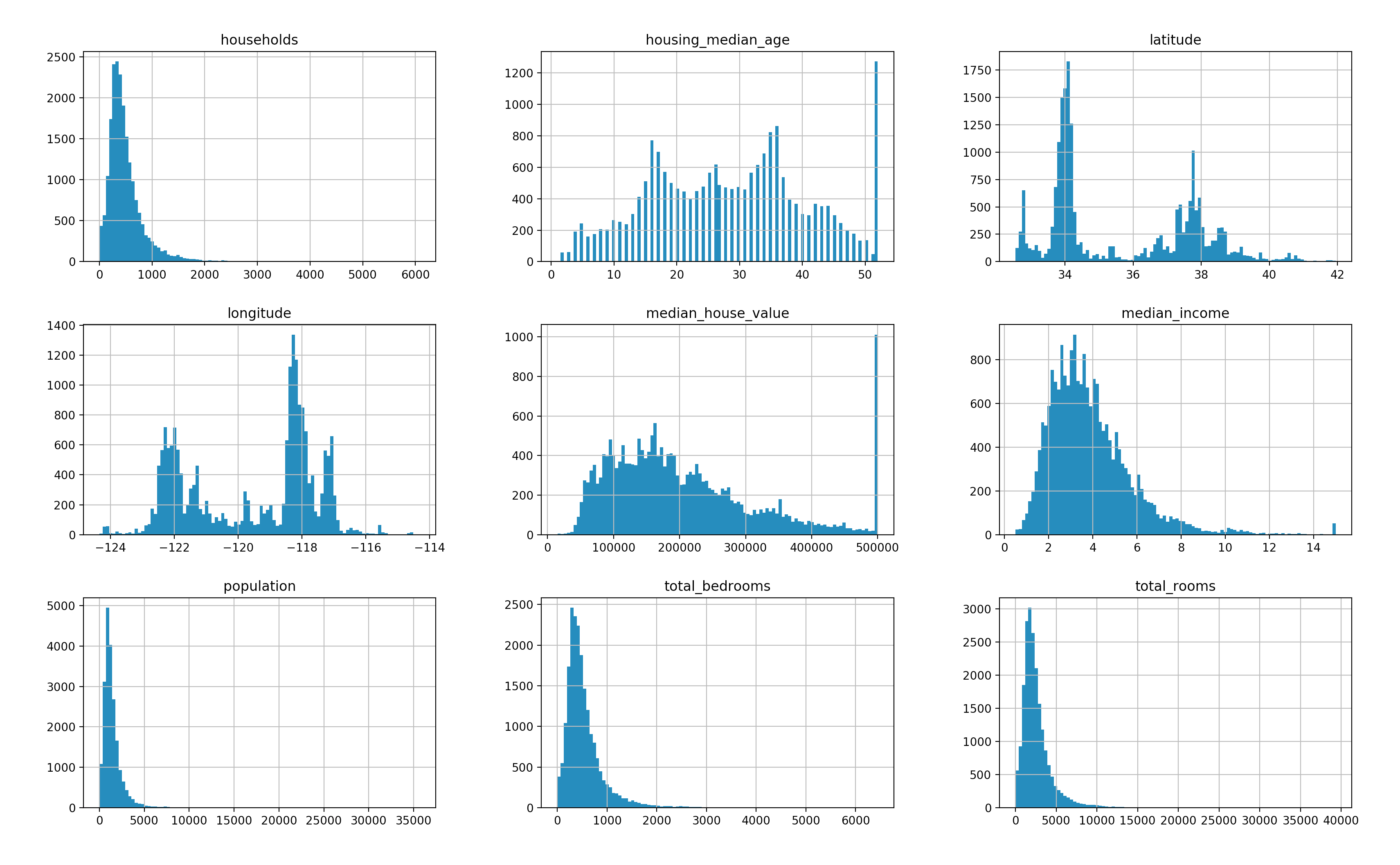
input_data.hist(bins=100, figsize=(20, 12))
plt.show()
这里会根据数据生成直方图,如下所示。从这幅图中我们可以看出数据的出现频度。
或者这样:
input_data.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
plt.show()
这里会根据经纬度生成散列点,同时我们设置了透明度为0.1,这样可以看出这些数据在地址位置上的密集程度。

预处理
现实中我们能够获取到的数据都是不完美的,通常都是会包含了一些无效值,或者值的缺失。上面这个数据中,也刚好是这样的。
在进行数据分析之前,我们第一步要做的就是对数据进行预处理。
fit和transform
scikit-learn提供了一系列的转换器(Transformer)。它们用来可以清理,减少,展开和生成特征表示。这些类会具有下面三个方法:
fit方法:该方法从训练集中学习模型参数(例如,用于归一化的均值和标准偏差)。transform方法:该方法对于数据进行模型变换。fit_transform方法:是前面两个方法的组合,它更加方便和高效。
sklearn.preprocessing中包含了一系列的工具进行数据的预处理。
下面我们就使用这些API来对上面的房价信息进行预处理。
处理字符串
数据中包含字符串不便于我们的分析,因此我们首先需要将字符串类型的数据转换成数值型数据。
我们可以使用LabelEncoder进行这项处理:
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
data["ocean_proximity"] = encoder.fit_transform(data["ocean_proximity"])
这里会对这列数据进行字符串到整数的转换,最后会转换成[0, 1, 2, 3…]这样的数据。
我们可以通过describe()了解下这列数据转换后的结果:
ocean_proximity
count 20640.000000
mean 1.165843
std 1.420662
min 0.000000
25% 0.000000
50% 1.000000
75% 1.000000
max 4.000000
处理无效值
前面我们看到了total_bedrooms列存在无效数据,其总共的有效数据只有20433条。
对于包含无效数据的单元,我们可以将其丢弃,或者用可能有效的值来填充。
sklearn.preprocessing.Imputer 就是用来进行数值填充的。它提供了下面三种策略:
- “mean”:通过有效数值的平均值来填充
- “median”:通过有效数值的中位数来填充
- “most_frequent”:通过有效数值中出现频度最高的值来填充
第1个和第3个策略大家都很好理解,但对于中位数有些人可能不太熟悉。
中位数是统计学中的专有名词,代表一个样本、种群或概率分布中的一个数值,其可将数值集合划分为相等的上下两部分。
下面是使用numpy获取平均值和中位数的代码示例:
import numpy as np
data = [1, 2, 3, 4, 5, 6, 7, 8, 95, 96, 97, 98, 100]
print("mean: {}".format(np.mean(data)))
print("median: {}".format(np.median(data)))
从输出可以看出,这个数据的平均值(mean)是40.153,而中位数(median)是7。
我们可以通过下面这段代码对原先包含无效数据的值进行填充,填充的测试是使用中位数。
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy="median")
X = imputer.fit_transform(data)
input_data = pd.DataFrame(X, columns=data.columns)
处理完成之后,我们可以查看处理完的数据以确认:
total_bedrooms
count 20640.000000
mean 536.838857
std 419.391878
min 1.000000
25% 297.000000
50% 435.000000
75% 643.250000
max 6445.000000
特性缩放
输入的数据值可能是各种范围的。例如median_house_value的最大值是500001。而housing_median_age只要两位数就可以描述。
有些情况下,有些数据的值可能非常大。而在做计算的时候,很容易发生溢出。在这种情况下,我们通常会对数据进行缩放。例如,对于[100, 10000]的数据,我们按比例缩放成[1, 100]。在保持数据比例的情况下,并不影响数据的处理结果。
MinMaxScaler用来通过指定数据的范围来进行数据的缩放。例如:
scalar = MinMaxScaler(feature_range=(0, 100), copy=False)
scalar.fit_transform(data)
便将所有的数据缩放的[0, 100]的范围之内了。
我们可以通过matplotlib的接口展示出处理前后的数据已进行对比:
plt.subplot(2, 1, 1)
plt.scatter(x=origin["longitude"], y=origin["latitude"],
c=origin["median_house_value"], cmap="viridis", alpha=0.1)
plt.subplot(2, 1, 2)
plt.scatter(x=scaled["longitude"], y=scaled["latitude"],
c=origin["median_house_value"], cmap="viridis", alpha=0.1)
plt.show()
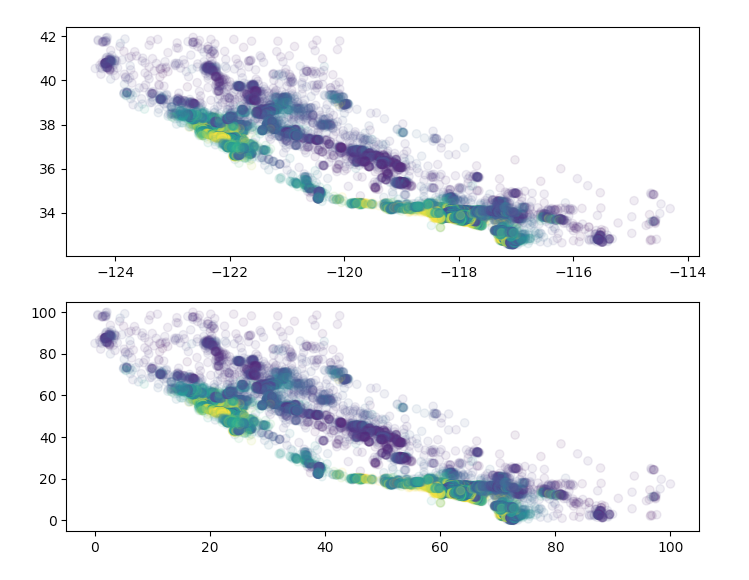
从这幅图中可以看出,这里我们仅仅是调整了数值的比例,而对于数据的分布并没有影响。
数据划分
为了得到预测模型,我们需要将所得到的数据划分成训练集和测试集两个部分。
前者用来训练数据模型,后者用来对于模型进行测试和验证。通常情况下,我们会用大部分的数据来训练,小部分的数据来测试。
在进行数据划分的时候,我们应该做到尽可能的“随机”。即:训练集和测试集都能尽可能的反应真实的数据模型。
permutation
permutation是numpy提供的接口。它将指定范围内的整数打乱以生成随机数。下面是一段代码示例:
import numpy as np
data = np.arange(0, 100)
np.random.seed(59)
print(data[np.random.permutation(100)[90:]])
这里我们将[0, 100)范围内的100个随机数进行了打乱。在打乱前通过np.random.seed(59)设置了随机数的种子,这样保证生成的随机数是稳定的。
最后我们打印出了打乱后数据的最后10个:
[64 67 0 57 53 79 23 77 44 49]
有了这些打乱的整数,我们便可以以此为索引来从已有的数据集中删选出训练集和测试集。例如:[0, 90]作为训练集,[90:]作为测试集。
train_test_split
sklearn也提供了类似的功能。这个函数就是train_test_split。代码示例如下:
import numpy as np
from sklearn.model_selection import train_test_split
data = np.arange(0, 100)
train_set, test_set = train_test_split(data, test_size=0.1, random_state=59)
print("test_set: \n {} \n".format(test_set))
这里的test_size指定了测试集的比例,random_state指定了随机数的种子。
这个函数会返回train_set和test_set两个集合。前者占90%的数据,后者占10%。我们打印出了测试集的数据结果:
test_set:
[38 46 24 87 30 85 16 96 18 99]
对于房价的数据,我们可以通过下面的方法将其分为训练集和测试集两部分:
train_set, test_set = train_test_split(input_data,
test_size=0.1, random_state=59)
show_data_summary(test_set)
最后一行打印出了测试集的数据,我们可以观察一下结果与我们的预期是否一致:
Describe Data:
longitude latitude housing_median_age total_rooms \
count 2064.000000 2064.000000 2064.000000 2064.000000
mean 48.415061 32.276916 53.952918 6.692606
std 19.640685 22.608316 24.649983 5.817431
min 0.896414 0.000000 1.960784 0.022890
25% 27.863546 14.665250 33.333333 3.638919
50% 58.764940 17.959617 54.901961 5.348695
75% 63.346614 54.835282 70.588235 7.932118
max 96.613546 98.618491 100.000000 82.977262
total_bedrooms population households median_income \
count 2064.000000 2064.000000 2064.000000 2064.000000
mean 8.309936 4.013810 8.192199 22.725069
std 6.794665 3.581933 6.626166 12.800111
min 0.062073 0.028028 0.049334 0.000000
25% 4.527467 2.149724 4.534616 13.727052
50% 6.719429 3.188150 6.610755 20.242479
75% 9.970515 4.904846 9.965466 28.686501
max 100.000000 80.055495 100.000000 100.000000
median_house_value ocean_proximity
count 2064.000000 2064.000000
mean 38.343739 28.234012
std 23.628904 34.874180
min 1.546592 0.000000
25% 20.350638 0.000000
50% 32.412444 25.000000
75% 49.432992 25.000000
max 100.000000 100.000000
First 10 rows:
longitude latitude housing_median_age total_rooms total_bedrooms \
9878 24.800797 43.464400 70.588235 0.854570 1.675978
4356 59.661355 16.471838 72.549020 5.483494 9.016139
1434 23.107570 57.810840 84.313725 3.184292 3.895096
6422 63.247012 16.896918 45.098039 6.566967 8.054004
1624 22.011952 56.323061 45.098039 5.414823 5.307263
1423 22.908367 58.023379 29.411765 2.754464 3.351955
4853 60.258964 15.834219 70.588235 7.068010 11.871508
16893 19.621514 53.560043 100.000000 4.328806 3.491620
4232 60.258964 16.578108 70.588235 13.487461 30.710739
19083 18.625498 61.424017 80.392157 5.351239 8.255742
population households median_income median_house_value \
9878 0.639031 1.628022 14.009462 19.237240
4356 2.965330 9.472126 16.995628 70.164865
1434 1.387371 3.552047 20.366616 27.608340
6422 5.229967 8.255221 19.201114 31.340283
1624 2.441212 6.117415 35.413305 70.226721
1423 0.989378 3.798717 12.732928 12.371289
4853 7.239553 11.971715 9.355043 35.567070
16893 1.872250 3.979609 54.968207 100.000000
4232 10.908377 30.800855 10.808816 55.319566
19083 3.189551 7.301431 18.020441 27.690814
ocean_proximity
9878 0.0
4356 0.0
1434 75.0
6422 25.0
1624 75.0
1423 75.0
4853 0.0
16893 100.0
4232 0.0
19083 0.0
....
线性模型(linear model)
我们可以从只包含一个属性值的数据集为起点来帮助我们理解线性模型。
现在假设我们要预测某个指定地区的房屋单价。在其他所有因素都相同的情况下,我们假设房价只与年代有关。
假设下面是已有的房价数据:
- 1999年,3800
- 2000年,3900
- 2001年,4000
- 2002年,4200
- 2003年,4500
- 2004年,5500
- 2005年,6500
- 2006年,7000
- 2007年,8000
- 2008年,8200
- 2009年,10000
- 2010年,14000
- 2011年,13850
- 2012年,13000
- 2013年,16000
- 2014年,18500
我们可以通过matplotlib将这个数据展示出来:
# house_price.py
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
data = pd.DataFrame({
"Year": [1999,2000,2001,2002,2003,2004,2005,2006,
2007,2008,2009,2010,2011,2012,2013,2014],
"Price": [3800,3900,4000,4200,4500,5500,6500,7000,
8000,8200,10000,14000,13850,13000,16000,18500]})
data.plot(kind="scatter", x="Year", y="Price", c="B", s=100)
plt.show()
这段代码得到的结果如下所示:
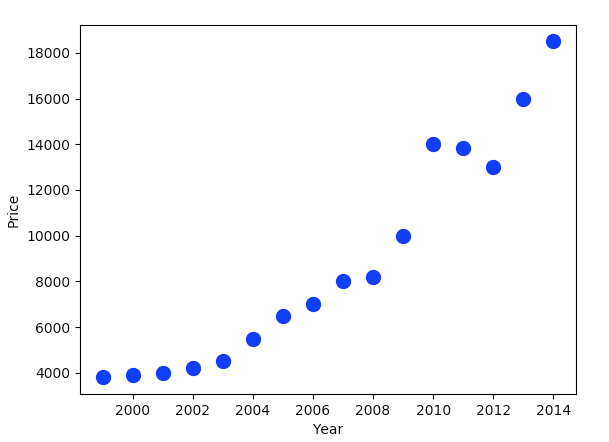
而如果我们想要预测2015年以及之后的房价,我们需要做的是:找到一条线,使得所有现在已有的点都能够尽可能的贴近这条线,根据这条线的走势,我们便可以预测未来的房价了。例如,下面这三条线都可以作为备选。
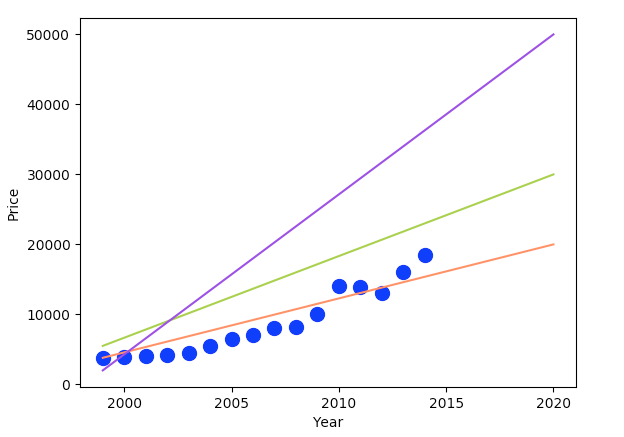
我们知道,直线的方程是:
\[f(x) = wx + b\]而我们只要确定w和b,这条直线就确定了。
实际上,决定房价的因素有很多。远远不止年代这一个因素。在实际的工程中,数据的属性甚至可能有成千上万个。所以我们需要将上面的模型,扩展到多个属性。
给定由n个属性描述的数据 $ x = (x_{1};x_{2};…;x_{n}) $,其中$x_{i}$是第i个属性上的取值。
线性模型试图学得一个通过属性的线性组合来进行预测的函数,即:
\[f(x) = w_{1}x_{1} + w_{2}x_{2} + ... + w_{n}x_{n} + b\]如果我们用向量$ x = (x_{1};x_{2};…;x_{n}) $和$ w = (w_{1};w_{2};…;w_{n}) $来代替,则可以将上面的函数写成这样:
\[f(x) = w^Tx + b\]而学习的目的就是确定w(向量)和b,这样模型就得以确定了。
回到这个具体的例子,每条数据包含十个值,其中median_house_value是我们要预测的结果。其他9个就是数据的特征。我们的目标是希望找到一个模型,能够通过其他9个属性来预测median_house_value的值。
写出算法以确定w(向量)和b的值并不是一件容易的事。好在scikit-learn中已经包含了相应的算法帮我们完成这个工作,我们只要直接使用即可。
首先,我们定义一个函数将需要预测的目标值与其他9个属性分离开:
def split_house_value(data):
value = data["median_house_value"].copy()
return data.drop(["median_house_value"], axis=1), value
接着我们使用这个函数将训练集和测试集的数据进行分离:
train_set, test_set = train_test_split(input_data,
test_size=0.1, random_state=59)
train_data, train_value = split_house_value(train_set)
test_data, test_value = split_house_value(test_set)
再下一步我们就可以通过训练集来训练模型了:
from sklearn.linear_model import LinearRegression
linear_reg = LinearRegression()
linear_reg.fit(train_data, train_value)
是的,短短的三行代码就完成了训练的工作。有了训练好的模型我们就可以用它来进行数据的预测了。这也仅仅只需要一行代码即可:
predict_value = linear_reg.predict(test_data)
最后,我们可以将预测出的结果与实际结果进行对比。以确认我们的预测结果是否准确:
def show_predict_result(test_data, test_value, predict_value):
ax = plt.subplot(221)
plt.scatter(x=test_data["longitude"], y=test_data["latitude"],
s=test_value, c="dodgerblue", alpha=0.5)
plt.subplot(222)
plt.hist(test_value, color="dodgerblue")
plt.subplot(223)
plt.scatter(x=test_data["longitude"], y=test_data["latitude"],
s=predict_value, c="lightseagreen", alpha=0.5)
plt.subplot(224)
plt.hist(predict_value, color="lightseagreen")
plt.show()
在这个函数中,我们针对实际结果和预测结果各绘制了一个散点图和一个直方图。实际结果是蓝色的,预测结果是绿色的。散点图的点代表数值的大小,而直方图中能看出数值的出现频度。
其结果如下图所示:
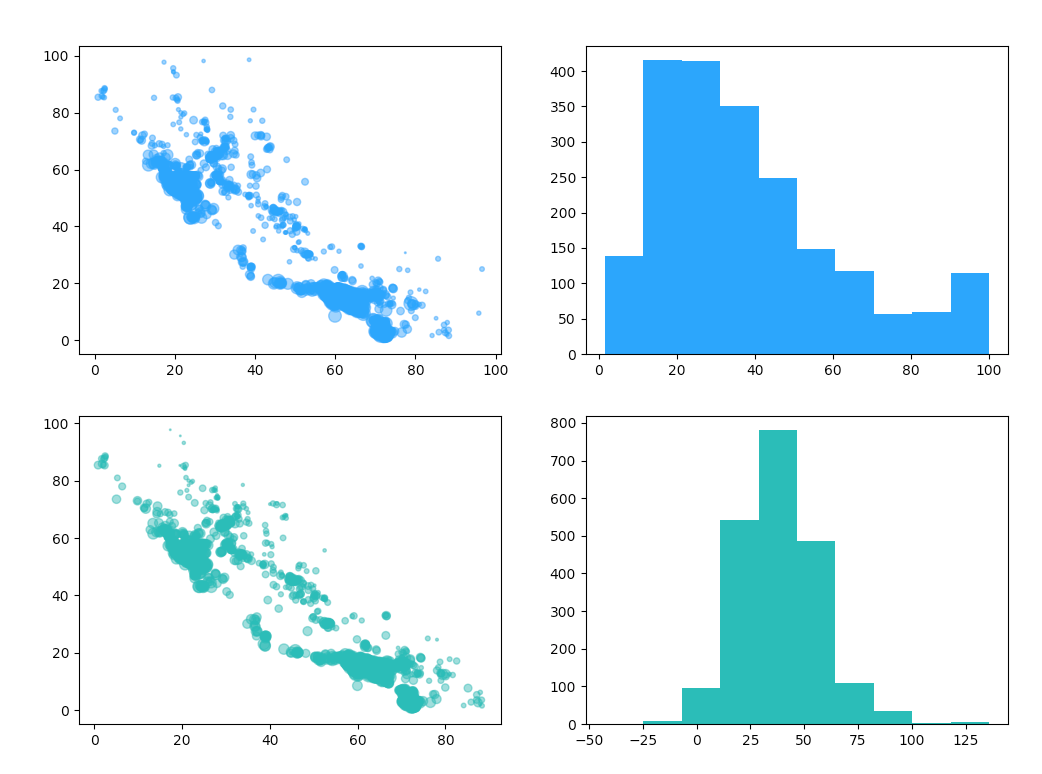
性能度量
刚刚我们以图示的方式对比了预测出来的结果和真实的结果。这种方法只能作为训练过程中辅助手段。因为这个结果需要人为去“看”,而且我们评价的结果也就是“还行”,“比较差”这样很主观的判断。真实的生产环境或者实验环境中当然需要更精准的度量方法。
均方误差
回归任务最常用的性能度量是均方误差(mean squared error,简称MSE),其计算方法如下所示:
\[E(f) = \frac{1}{m}\sum_{i=1}^{m}(f(x_{i})-y_{i})^2\]这个算法是将预测值与实际值相减求平方,然后对所有的平方结果取平均值。
有了scikit-learn之后我们就不用自己实现这个算法了,直接调用mean_squared_error函数即可:
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(test_value, predict_value)
print("Diff: {}".format(np.sqrt(mse)))
这个函数的第一个参数是真实的结果,第二个是预测出的结果。将得到的数值开平方之后得到的结果是:
Diff: 14.127834130789983
这样我们便知道了模型的精确结果:在[0, 100]之间区间上预测结果误差有14左右。
交叉验证
scikit-learn中还提供了交叉验证算法。
这种算法将训练集随机分为n份(称之为fold),然后每次选取其中的一份作为结果,其他n-1份作为训练。以此来计算算法的得分。因此这种算法最后会返回n个结果。每个结果都是一个数字类型的得分。
代码示例如下:
from sklearn.model_selection import cross_val_score
scores = cross_val_score(linear_reg, train_data, train_value, cv=10)
print("cross_val_score: {}".format(scores))
结果如下:
cross_val_score: [0.65629302 0.67609342 0.60996658 0.64629956 0.64577402 0.64565816
0.62451489 0.57967974 0.62916854 0.60401622]
如果我们有多个模型,我们便可以很方便的通过对比得分来对比这两种模型。
注:该函数详细说明见这里:cross_val_score
结束语
至此,我们关于线性回归的第一篇内容就结束了。
本文牵涉的内容并不少,可能需要一些时间来消化。
在下一篇文章中,我们会讲解scikit-learn与分类预测的相关内容。
敬请期待。