本文是scikit-learn系列文章的第二篇,会讲解分类预测的相关知识,并会给出通过scikit-learn进行分类预测的代码示例。强烈建议读者在读本文之前先阅读前一篇文章:《使用scikit-learn进行线性回归分析》
分类任务介绍
分类预测是机器学习中非常常见的一项任务。前面我们已经知道,分类任务的目标是将输入向量分配给有限数量的离散类别之一。例如:
- 预测某个人会不会得癌症
- 识别图片的内容是哪个字母或者数字
这其中,第一个问题是二分类问题,预测的结果只有正例和反例两种情况。第二个问题是多分类问题,需要预测出具体是哪个分类。
多分类
多分类(Multiclass)问题是非常常见的,例如识别出某个手写的数字(0~9中的一个),分析某个人属于哪个国籍。
有些算法本身就可以处理多分类问题,例如随机森林(Random Forest)和朴素贝叶斯(naive Bayes)分类器。而另外一些算法只能处理二分类问题,例如支持向量机(Support Vector Machine)或者线性分类器。
我们可以通过一些策略来利用二分类学习器解决多分类问题,这些策略的基本思路是“拆解法”。
最常见的拆解法是下面两种:
- 一对其余(One-versus-Rest,简称OvR,或者One-versus-all,简称OvA)
- 一对一(One-versus-One,简称 OvO)
考虑对于有 $ C_{1},C_{2},…,C_{N} $一共N个分类的问题。第一种方法需要N个分类器,第二种方法则需要$ N * (N-1)/2 $个分类器。
以数字识别为例。对于第一种方法需要10个分类器,已确认具体的某个用例是否是数字0,1,2,…,9。然后我们会选出可能性最大的作为预测结果。
而对于第二种方法,我们一共需要下面45个分类器:
- 0 vs. 1
- 0 vs. 2
- …
- 1 vs. 0
- 1 vs. 2
- …
- 9 vs. 7
- 9 vs. 8
这两种拆解法对比如下图所示:
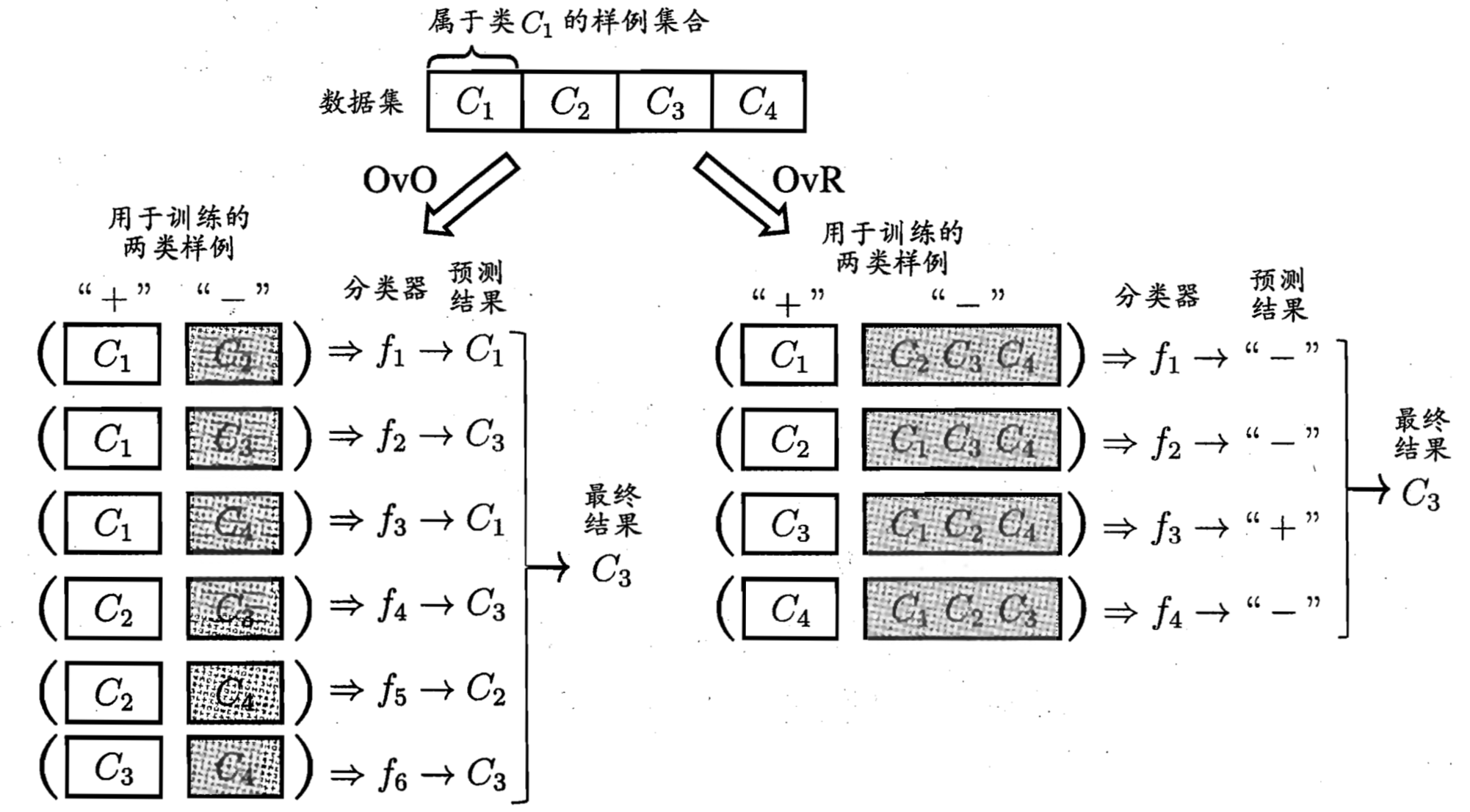
上图取自周志华《机器学习》第三章。
多标签分类
有些情况下,对于用例的分类可能是多个结果。例如:对于包含多个人物的照片的人脸识别;或者是预测某个人可能会生哪些疾病。这种情况称之为多标签分类(Multilabel Classification)。
实验描述
本文中我们将根据一组真实的数据预测乳腺癌的发生。
数据的主页见这里:Breast Cancer Wisconsin (Original) Data Set
数据的说明见这里:breast-cancer-wisconsin.names
数据文件可以在这里获取:breast-cancer-wisconsin.csv
注:sklearn_tutorial项目源码中也包含了这个数据文件。
下面是数据的前20列:
| A | B | C | D | E | F | G | H | I | J | K |
|---|---|---|---|---|---|---|---|---|---|---|
| 1000025 | 5 | 1 | 1 | 1 | 2 | 1 | 3 | 1 | 1 | 2 |
| 1002945 | 5 | 4 | 4 | 5 | 7 | 10 | 3 | 2 | 1 | 2 |
| 1015425 | 3 | 1 | 1 | 1 | 2 | 2 | 3 | 1 | 1 | 2 |
| 1016277 | 6 | 8 | 8 | 1 | 3 | 4 | 3 | 7 | 1 | 2 |
| 1017023 | 4 | 1 | 1 | 3 | 2 | 1 | 3 | 1 | 1 | 2 |
| 1017122 | 8 | 10 | 10 | 8 | 7 | 10 | 9 | 7 | 1 | 4 |
| 1018099 | 1 | 1 | 1 | 1 | 2 | 10 | 3 | 1 | 1 | 2 |
| 1018561 | 2 | 1 | 2 | 1 | 2 | 1 | 3 | 1 | 1 | 2 |
| 1033078 | 2 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 5 | 2 |
| 1033078 | 4 | 2 | 1 | 1 | 2 | 1 | 2 | 1 | 1 | 2 |
| 1035283 | 1 | 1 | 1 | 1 | 1 | 1 | 3 | 1 | 1 | 2 |
| 1036172 | 2 | 1 | 1 | 1 | 2 | 1 | 2 | 1 | 1 | 2 |
| 1041801 | 5 | 3 | 3 | 3 | 2 | 3 | 4 | 4 | 1 | 4 |
| 1043999 | 1 | 1 | 1 | 1 | 2 | 3 | 3 | 1 | 1 | 2 |
| 1044572 | 8 | 7 | 5 | 10 | 7 | 9 | 5 | 5 | 4 | 4 |
| 1047630 | 7 | 4 | 6 | 4 | 6 | 1 | 4 | 3 | 1 | 4 |
| 1048672 | 4 | 1 | 1 | 1 | 2 | 1 | 2 | 1 | 1 | 2 |
| 1049815 | 4 | 1 | 1 | 1 | 2 | 1 | 3 | 1 | 1 | 2 |
| 1050670 | 10 | 7 | 7 | 6 | 4 | 10 | 4 | 1 | 2 | 4 |
| 1050718 | 6 | 1 | 1 | 1 | 2 | 1 | 3 | 1 | 1 | 2 |
| … |
每一列的说明如下:
| 列 | 说明 | 数值 |
|---|---|---|
| A | Sample code number | Number |
| B | Clump Thickness | 1 - 10 |
| C | Uniformity of Cell Size | 1 - 10 |
| D | Uniformity of Cell Shape | 1 - 10 |
| E | Marginal Adhesion | 1 - 10 |
| F | Single Epithelial Cell Size | 1 - 10 |
| G | Bare Nuclei | 1 - 10 |
| H | Bland Chromatin | 1 - 10 |
| I | Normal Nucleoli | 1 - 10 |
| J | Mitoses | 1 - 10 |
| K | Class | 2:良性;4:恶性 |
这里我们要预测的是第K列数据。它存在两种可能的取值:
- 2 表示良性肿瘤
- 4 表示恶性肿瘤
所以实际上这是一个二分类问题:只有正例和反例两种情况。
实验环境
本文的代码在如下环境中测试:
- Apple OS X 10.13
- Python 3.6.3
- scikit-learn 0.19.1
- matplotlib 2.1.1
- numpy 1.13.3
- graphviz 0.8.3
本文中的源码和测试数据可以在这里获取:sklearn_tutorial
实验数据
实验的数据是一个csv文件,所以很显然我们可以通过pandas的接口读取这些数据。数据中包含了一些值的缺失,我们还需要对这些无效值进行处理。下面是获取数据的代码:
# lession2_classification.py
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.preprocessing import Imputer
def prepare_data():
input_data = pd.read_csv("./data/breast-cancer-wisconsin.csv",
names=['id', 'clump_thickness', 'cell_size', 'cell_shape',
'marginal_adhesion', 'single_cell_size', 'bare_nuclei',
'bland_chromatin', 'normal_nucleoli', 'mitoses', 'class'])
input_data = input_data.apply(pd.to_numeric, errors='coerce')
imputer = Imputer(strategy="mean")
X = imputer.fit_transform(input_data)
return pd.DataFrame(X, columns=input_data.columns)
在这段代码中,我们通过read_csv函数读取了csv文件,同时指定了每一列的列名。之后,我们通过to_numeric函数将数据转换成数字类型,同时将无效值设置为NaN。关于to_numeric函数的详细说明请参见官方文档:pandas.to_numeric。
在这之后,我们借助于Imputer通过平均数填充了无效值。
在读取到数据之后,我们需要将数据分为训练集和测试集两个部分。这里我们直接使用之前介绍过的train_test_split函数即可:
# lession2_classification.py
from sklearn.model_selection import train_test_split
def data_split(input_data):
target = input_data['class'].copy()
return input_data.drop(['class'], axis=1), target
if __name__ == '__main__':
input_data = prepare_data()
train_set, test_set = train_test_split(input_data,
test_size=0.1, random_state=59)
train_data, train_value = data_split(train_set)
test_data, test_value = data_split(test_set)
这里我们还定义了data_split函数用来将需要预测的结果与其他数据分开。最后我们得到的数据是:
- train_data:训练集的数据
- train_value:训练集的结果
- test_data:测试集的数据
- test_value:测试集的结果
后面我们将通过train_data和train_value来训练算法,然后根据test_data来预测结果,并与test_value对比进行结果的度量。
如果你对这里的代码不理解,请返回阅读前一篇文章:《使用scikit-learn进行线性回归分析》
性能度量
前一篇文章讲解线性回归的时候,我们介绍了均方误差和交叉检验两种度量方法。
而对于分类任务,有下面几种度量方法。
迷惑矩阵与精度
这种度量方法既适用于二分类任务,也适用于多分类任务。
迷惑矩阵(Confusion Matrix)是一个矩阵。下面是一个示例(数据来自Wikipedia:Confusion matrix):
| Cat | Dog | Rabbit | |
|---|---|---|---|
| Cat | 5 | 2 | 0 |
| Dog | 3 | 3 | 2 |
| Rabbit | 0 | 1 | 11 |
这个矩阵的行数据表示预测的结果,列数据表示用例的真实分类。对于上面示例解读如下:
- 有7(5+2)个用例被分类为Cat,其中有2个是错误的,它们的真实分类是Dog。
- 有8(3+3+2)个用例被分类为Dog,其中有5个是错误的,其中有3个是Cat,有2个是Rabbit。
- 有12(1+11)个用例别分类为Rabbit,其中有1个用例是错误的,它的真实分类是Dog。
精度是分类正确的样本占样本总数的比例。对应的,还有错误率,错误率是分类错误的样本数占样本总数的比例。
很显然:
\[精度 = 1 - 错误率\]以上面的示例来说,该结果的精度是$\frac{5+3+11}{5+2+3+3+2+1+11} = \frac{19}{27} = 0.704$,错误率是$\frac{8}{27} = 1-0.704 = 0.296$。
查准率与查全率
对于二分类问题,我们还有专门的度量方法。
在二分类的场景下,有正例和反例(例如:是否有得癌症的可能)两种情况。而对于预测的结果来说,也有预测对和错两种情况。所以综合起来一种有下面四种可能:
| 真实结果 | 预测为反 | 预测为正 |
|---|---|---|
| 反例 | TN(真反例) | FP(假正例) |
| 正例 | FN(假反例) | TP(真正例) |
在不同的场景下,我们的目标可能是不一样的。
例如:在为儿童过滤18禁内容的场景下,我们宁愿将正常的内容误判为不适合,也不能将色情内容漏判为可以观看的内容。即,不能接受假正例存在。
而在电商平台为用户推荐商品的时候,我们希望的是足够多的推荐商品列表。并且是允许出现一些用户可能并不关心的商品的。即:能够接受假正例的存在。
这就是查准率(Precision)与查全率(Recall)存在的意义了。
查准率指的是:在选中的正例中,有多少是真正的正例。公式如下:
\[P = \frac{TP}{(TP + FP)}\]查全率(也叫召回率)指的是:在所有的正例中,有多少被选出来了。公式如下:
\[R = \frac{TP}{(TP + FN)}\]并且,通常情况下,这两者是互相矛盾的。以筛选出用户感兴趣的商品为例,当我们尽可能多的增加商品列表的时候,查全率会上升,但是查准率则可能会下降(虽然用户感兴趣的商品全部被选出来了,但也可能增加了很多用户并不感兴趣的商品)。
F1值
查准率和查全率是两个数值,我们能不能把它们综合起来,以综合后的结果来衡量不同的算法呢?
答案是肯定的,这个值就是F1($F_1$ score,也称F-score,F-measure),计算它的公式如下:
\[F1 = \frac{2}{\frac{1}{recall} + \frac{1}{precision}} = 2 * \frac{precision * recall}{precision + recall}\]Classification metrics 中包含了用来对分类器进行性能度量的API。
下面是我们代码示例中定义的函数:
# lession2_classification.py
import pandas as pd
from sklearn.preprocessing import LabelBinarizer
from sklearn.metrics import f1_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
def measure_predict(y_true, y_predict):
lb = LabelBinarizer()
bin_true = pd.Series(lb.fit_transform(y_true)[:,0])
bin_predict = pd.Series(lb.fit_transform(y_predict)[:,0])
print("confusion matrix: \n{}\n".format(
confusion_matrix(bin_true, bin_predict)))
print("recall_score: {}\n".format(
recall_score(bin_true, bin_predict)))
print("precision_score: {}\n".format(
precision_score(bin_true, bin_predict)))
print("f1_score : {}\n".format(
f1_score(bin_true, bin_predict)))
这个函数的输入是:
y_true:真实的结果y_predict:算法预测的结果
在本实验中,算法的结果是2或者4。所以我们通过LabelBinarizer将其转换成0和1的形式。因为只有这样才可以计算查询率和F1值(这两个概念针对二分类问题才有意义)。
对数回归
有些回归算法可以用来完成分类任务(同样,有些分类算法也可以用来执行回归任务),对数回归(英文是Logistic Regression,Logistic的意思是”对数的“,而不是”逻辑“)便是其中一种。虽然名称是”回归“,但实际上这是一个二分类方法(好奇心重的读者肯定要问为什么,那就看看这里:Why isn’t Logistic Regression called Logistic Classification?)。
我们在前一篇文章中介绍了线性回归,它的预测结果是连续的值。而二分类问题的预测结果是只有正例反例两种情况中的一种,可以记为 y ∈ {0, 1}。 所以对于回归的预测值z我们可以规定:
- 如果 z < 0, y = 0
- 如果 z > 0, y = 1
(如果z=0,我们可以任意规定y取0或者1。)
但这个规则表示成函数是阶跃函数它是不连续的。因此我们希望能够找到在一定程度上近似这个规则的”替代函数“。而下面这个函数刚好满足:
\[y = \frac{1}{1+e^{-z}}\]而这个函数就是对数几率函数(logistic function)。它的图形如下:
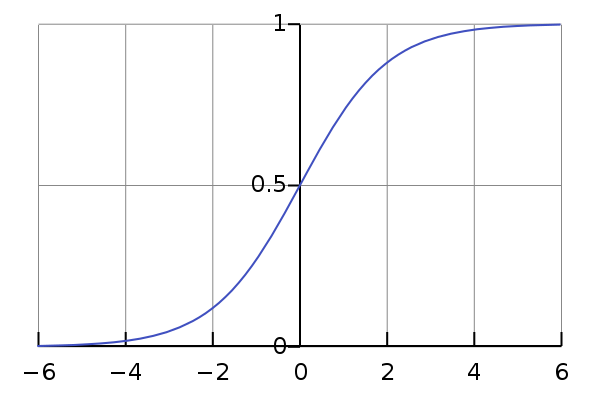
当z很大时,y无限接近于1。当z很小时,y无线接近于0。
我们可以将线性函数带入这个函数中,得到下面这个函数:
\[y = \frac{1}{1+e^{-(w^{T}x+b)}}\]scikit-learn API
当然,有了scikit-learn之后我们不必自己实现这些复杂的算法了。直接使用它提供了API即可:
# lession2_classification.py
from sklearn.linear_model import LogisticRegression
def logistic_reg(train_data, train_value, test_data):
logReg = LogisticRegression()
logReg.fit(train_data, train_value)
return logReg.predict(test_data)
决策树
实际上,决策树(Desicion Tree)是我们都非常熟悉的一个概念,因为我们在生活中经常用到这个算法。
假设我们得到了一笔意外的奖金,而这笔奖金我们只能选择买一样东西,那么我们会怎么选呢?下面是我们可能存在的心理过程:
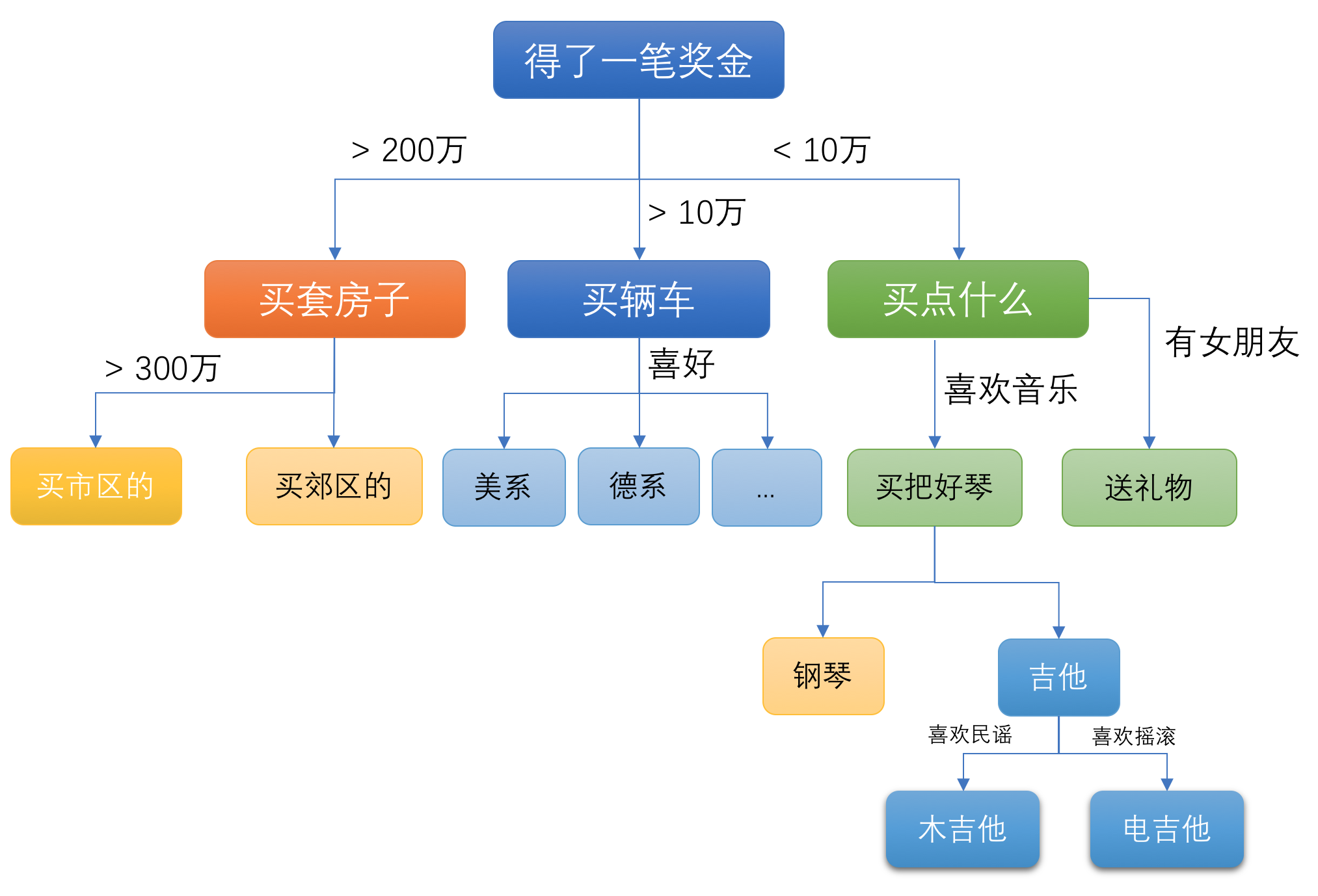
看见没有?我们决策的过程就是树状的结构,根据一些外部的条件和自己的选择最终走到某一个分支上(当然,对于购买东西来说,结果可能是多选的,但对于某个数据分类的预测,在分类之间互相独立的情况下,最终的结果最多只会有一个)。
在使用决策树模型进行分类预测时,决策树的叶子节点是确切的某个分类,内部节点是数据的属性。
有些读者自然会问,这里选择了奖金金额作为第一个考虑因素,那为什么我不能选择其他因素(譬如有没有女朋友)呢?
在我们构建决策树的时候,最重要的问题就是树中分支的顺序:要先考虑什么属性,再考虑什么属性。例如,考虑这样一种场景:根据树叶的图形预测这是什么树的叶子。在这种情况下,树叶的颜色,大小,形状,纹理等等,都是数据的属性,因此将是我们构成决策树内部节点的基础。
回到本文要分析某个人是否可能有乳腺癌的问题也是一样,B ~ J列的数据都是我们需要考虑的生成内部节点的地方。那我们该如何选择和排序呢?我们的本能反应就是:根据属性的“重要性”排序,依次考虑每一个属性来进行判断和选择。
那么,属性的重要性该如何度量呢?
熵与相对熵(信息增益)
熵这个词的英文原文是Entropy,它的含义是:混乱,无序,不确定性。
是不是觉得这个词很难理解?据说,熵之所以叫做“熵”就是因为”这个词别人不懂,很容易被唬住“
那么什么是有序,什么是无序呢?
考虑一个集合,如果集合中所有数据都属于同一个分类,那么这个集合就是有序的。相反的,如果每个数据都属于不同的分类,那就是无序的,混乱的。
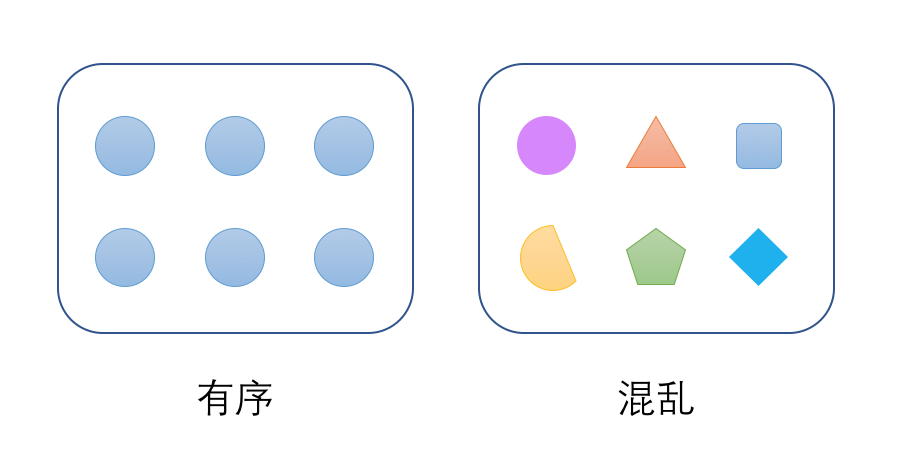
在这两种极端情况以外,再考虑另外一种情况。假设有两组人。第一组中有50%女生,50%男生。第二组有95%是女生,只有5%是男生。这两组数据那组更有序?
答案是第二组。因为,当我们从两组人中任意的挑一个人出来,对于第一组来说,ta是男是女各有一半的可能性。而对于第二组,我们会觉得ta非常可能是女生,毕竟概率有95%。
那我们该如何度量这种有序和无序呢?
伟大的数学家,信息论创始人香农(Claude Shannon) 已经为我们找到了公式。该公式定义如下。值越大表示数据越是混乱无序(从信息论的角度来说,也就意味着可以存储更多的信息,但是这个角度与我们这里要讨论的问题无关)。
\[Ent(D) = - \sum_{k=1}^{n}p_{k}log_{b}p_{k}\]公式中的b通常取值2,e或者10。下文我们统一取2。
不要被这个公式吓倒,这个公式其实只有两个变量需要解释:
- n是集合中数据分类的总数。例如:性别的分类只有2种。
- $p_k$是第k种数据出现的概率。例如:50%或者95%。
对于所有数据都是同一个分类的情况下,熵的计算如下:
$ Ent = -1log_{2}1 = 0 $
它的无序程度是0,所以可以反过来说:它是有序的。
然后,我们再计算一下刚刚提到的两组人群的熵各是多少。
对于第一组人群来说:
$ Ent(D1) = - \sum_{k=1}^{2}p_{k}log_{2}p_{k} = - (0.5* log_{2}0.5 + 0.5* log_{2}0.5) = - log_{2}\frac{1}{2} = 1 $
对于第二组人群来说:
$ Ent(D2) = - \sum_{k=1}^{2}p_{k}log_{2}p_{k} = - (0.95* log_{2}0.95 + 0.05* log_{2}0.05) = 0.0703 + 0.216 = 0.2863 $
可见第一组的熵更大,也就是更加混乱,无序。
请读者计算一下:在包含100个数据的集合里面,假设每个数据都各自属于不同的分类,这组数据的熵是多少?
再回到我们前面的问题:在构建决策树的时候,我们该如何构建树的分支呢?或者说,我们该如何考虑分支顺序,先考虑什么因素,再考虑什么因素呢?
决策树的分支源于数据的属性,例如:树叶的颜色,大小,形状,纹理。而对于本文的例子,也就是B ~ J列的数据。
答案就在于条件熵。熵定义了一个数据集合的混乱程度,而条件熵描述的是:在某个属性已经确定的情况下,集合的混乱程序。
例如:还是以根据树叶预测植物分类为例,假设得到的树叶只有梧桐树叶和松树叶两种。如果我们树叶的颜色,是很难区分的,因为它们可能都是绿色。但如果我们根据树叶的形状,那么就可以很明显的区分出来。即:在树叶形状已知的情况下,梧桐树叶和松树叶就很容易分类(有序)了。
条件熵的公式如下:
\[H(D|X) = - \sum_{k=1}^{v}p(D,X)log_{2}p(D|X)\]这里的D是集合整体,X是某个属性条件。这个值越小就表示:在某个属性确定的情况下,数据越有序。
除此之外,还有一个概念叫做相对熵,相对熵(relative entropy)又称为KL散度(Kullback–Leibler divergence,简称KLD),信息散度(information divergence),或者是信息增益(information gain)。
\[相对熵(信息增益) = 熵 - 条件熵\]相对熵反应了在考虑某个属性的基础上,对集合总体混乱程度的贡献,因此相对熵越大,就意味着我们应该越优先考虑这个属性来进行分类。
由此,我们可以计算出每个属性的相对熵(或者叫:信息增益),然后按照大小排序,便可以构建出我们需要的决策树了。
CART算法与基尼不纯度
构建决策树的算法不止一种。上面提到的内容由ID3,C4.5算法所使用。而scikit-learn使用的是称之为CART(Classification And Regression Tree)的算法。
由于篇幅所限,关于这些算法的详细说明和对比不再继续展开,有兴趣的读者可以以维基百科:Decision tree learning为起点继续探索。
CART算法是基于基尼不纯度(Gini impurity)为基础来构建决策树。Gini不纯度描述了集合数据的不一致性,和熵表达的概念是类似,这个值越大表示数据越不一致,或者说越不均匀。
它的计算公式如下:
\[G = \sum_{k=1}^n\sum_{k'≠k}p_{k}p_{k'} =1- \sum_{k=1}^{n}p_{k,k'}^2\]直观来说,基尼不纯度描述了:从一个集合中随机取两个样本,这两个样本不一致的概率大小。
经济学上用基尼系数(Gini Coefficient)来衡量一个地区的财富分配是否均匀。这是基尼不纯度本质上是一回事。
当我们在构建决策树的时候,就是根据属性的“纯度”来考虑分支的先后顺序的。我们应当优先选择纯度更高(基尼不纯度值更小)属性来进行划分。
对于集合D,属性a的基尼不纯度计算方法是:以属性a将集合分为v组,计算每组的基尼不纯度$D^v$。然后再应用下面的公式:
\[Gini\_index(D, a) = \sum_{v=1}^V\frac{D^v}{D}Gini(D^v)\]scikit-learn API
同样的,有了scikit-learn之后,我们不用自己实现这个公式的计算,直接调用它提供的API即可:
# lession2_classification.py
from sklearn.tree import DecisionTreeClassifier
def dicision_tree(train_data, train_value, test_data):
tree_clf = DecisionTreeClassifier(max_depth=5)
tree_clf.fit(train_data, train_value)
write_file(tree_clf)
return tree_clf.predict(test_data)
这里我们指定了决策树最多只允许5层。对于这个参数值的选择,请根据具体的问题来调优。
可视化
我们可以将决策树的结果导出的一个物理文件以观察算法的决策过程。下面是代码示例:
# lession2_classification.py
import graphviz
from sklearn.tree import export_graphviz
def write_file(tree_clf):
dot_data = export_graphviz(tree_clf, out_file=None,
filled=True, proportion=True, rounded=True)
graph = graphviz.Source(source=dot_data,
filename="./decision_tree", format="png")
graph.render()
这个函数会将结果导出到decision_tree.png文件中。
需要注意的是,这需要事先安装graphviz python包和graphviz系统命令包,前者提供Python接口,后面提供dot命令行工具。
关于如何安装这两个包,请自行在网上搜索,下面是我在OS X系统上安装的方法:
pip3 install graphviz
brew install graphviz
除了直接保存图片文件,在没有安装上面两个包的情况下,你也可以通过下面的方法将dot数据保存到文本文件中:
export_graphviz(tree_clf, out_file="./dot_data.txt", filled=True, proportion=True, rounded=True)
有了这个数据之后,可以借助其他工具将其转换成可视化的图,例如这个网站:WebGraphviz。
将dot_data.txt文本文件中的内容全部复制粘贴进去之后点击“Generate Graph!”按钮即可。
我们得到的图片会是下面这个样子:
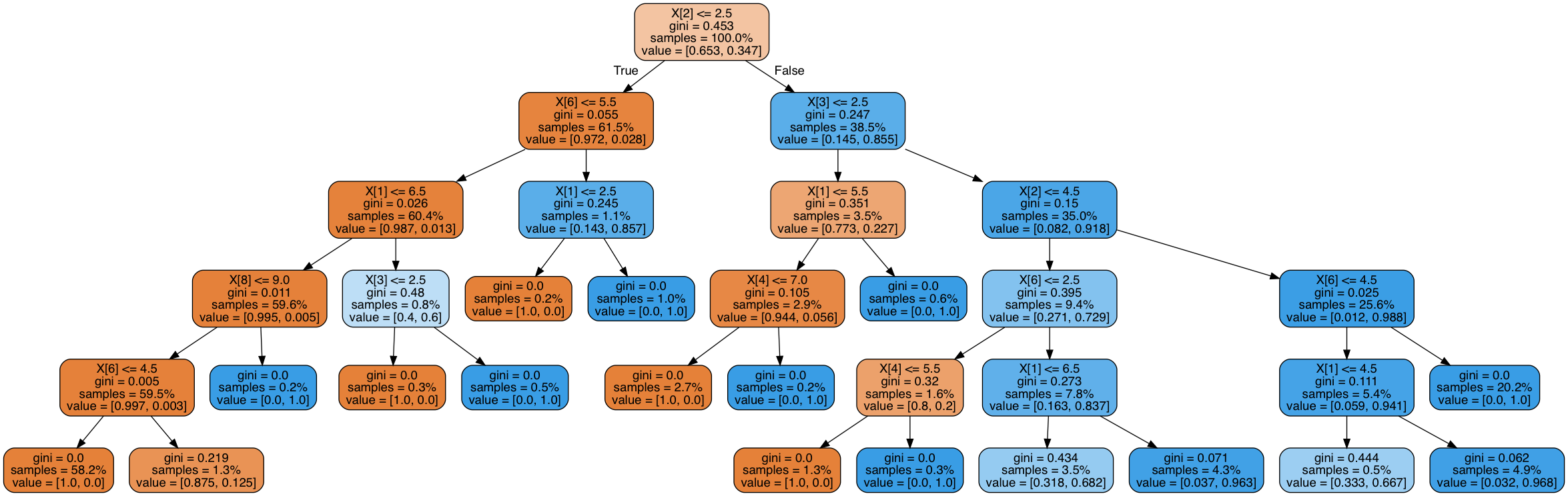
这个图比较大,你不一定能看清楚里面的所有内容。不过这不是重点,关键是你知道如何获取这个图,以及这个图大致的样子就可以了。
预测结果
在本文的代码示例中,对数回归的算法比较失败,其迷惑矩阵结果如下:
== logistic regression ==
confusion matrix:
[[47 0]
[23 0]]
即:它错过了所有的正例,所以计算其他的得分就没有什么意义了。
而决策树的结果还算不错:
== decision tree ==
confusion matrix:
[[44 3]
[ 2 21]]
recall_score: 0.9130434782608695
precision_score: 0.875
f1_score : 0.8936170212765957
它的结果是:
- 47个反例中误测了三个反例
- 23个正例中错过了两个正例
- 查全率是91.3%($\frac{21}{21+2}$)
- 查准率是87.5%($\frac{21}{21+3}$)
- F1得分是0.894
参考资料与推荐读物
- Decision tree learning
- Documentation of scikit-learn
- Classification And Regression Tree
- 决策树算法原理
- Information Gain
- 信息熵、信息增益与信息增益率
- Nando de Freitas CPSC 540 Machine learning - Decision trees
- Andrew Ng CS229 Lecture notes
- 《机器学习》- 周志华
- 《Hands-On Machine Learning with Scikit-Learn and TensorFlow》
- scikit-learn决策树算法类库使用小结